Магический квадрат виды сказуемых

Магический квадрат — виды, правила и примеры решения

История и современное применение

Первые подобные таблицы использовались ещё в Древней Греции и Китае. Это подтверждено археологическими находками. Арабы называли квадраты магическими, так как верили, что они обладают волшебными свойствами и могут защитить от многих напастей.

В середине XVI в. вопросом о том, как работает магический квадрат, заинтересовались математики в Европе. Они начали активно исследовать загадочные сочетания цифр. Учёные стремились вывести общие принципы построения квадратов и найти всё множество возможных вариантов.

В современной общеобразовательной школе разные виды магических квадратов используются на уроках математики. Они способствуют развитию логического мышления и вызывают у детей живой интерес.

С их помощью школьники учатся планировать свою работу и контролировать её. В клетки можно вписывать не только отдельные цифры, но и математические выражения. Задачи на эту тему часто предлагаются на математических олимпиадах. Решать такие числовые задачи можно и онлайн.

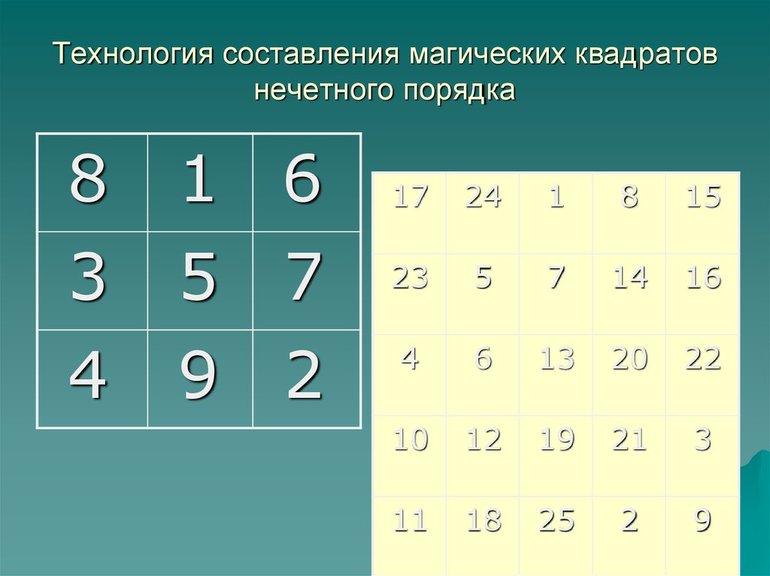
Квадрат нечётного порядка

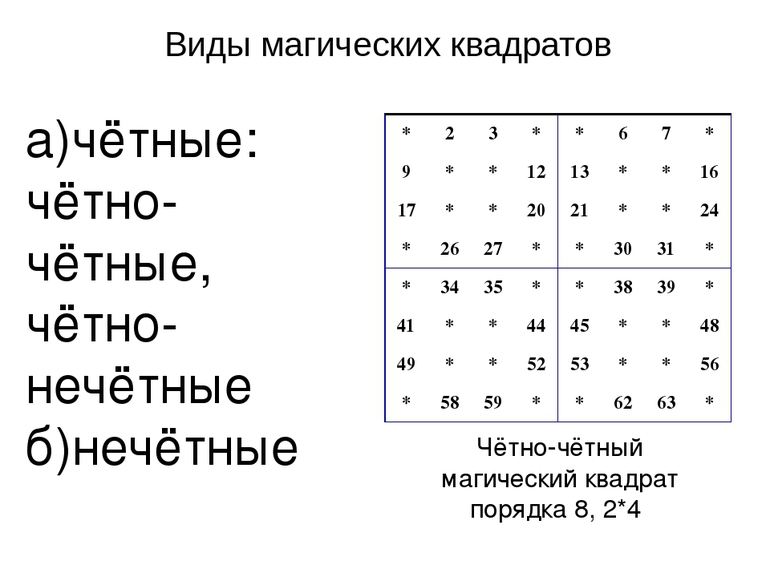
Среди несложных магических квадратов по математике выделяют разновидности чётного и нечётного порядка. Первая группа подразделяется на таблицы одинарной и двойной чётности.

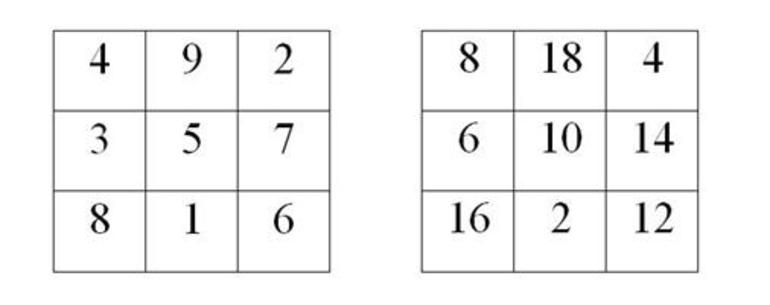
Начальным шагом во всех случаях будет определение магической константы. Делается это с помощью специальной формулы [n * (n2 + 1)] / 2. Разобраться с принципом решения задачи этого класса можно на самом простом примере. Для этого выстраивается таблица из 9 ячеек. В неё нужно расставить цифры от 1 до 9. Дальнейший алгоритм:

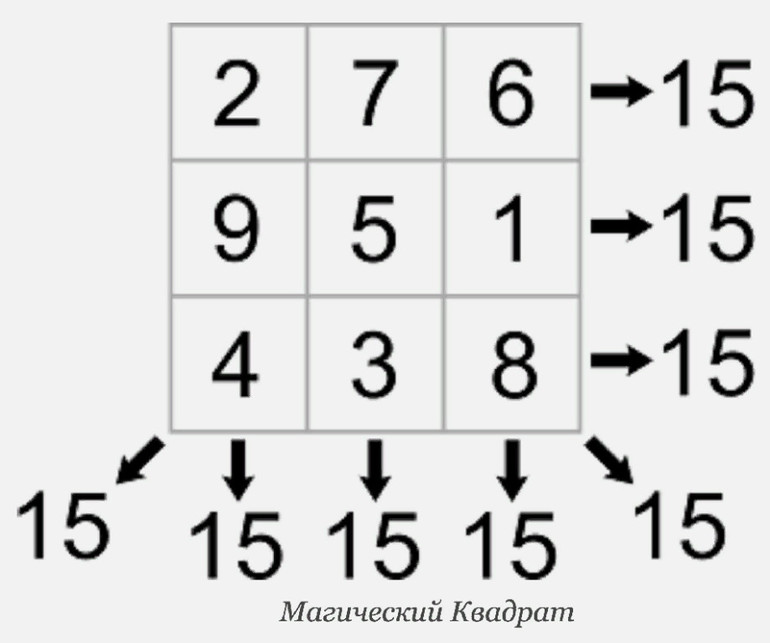
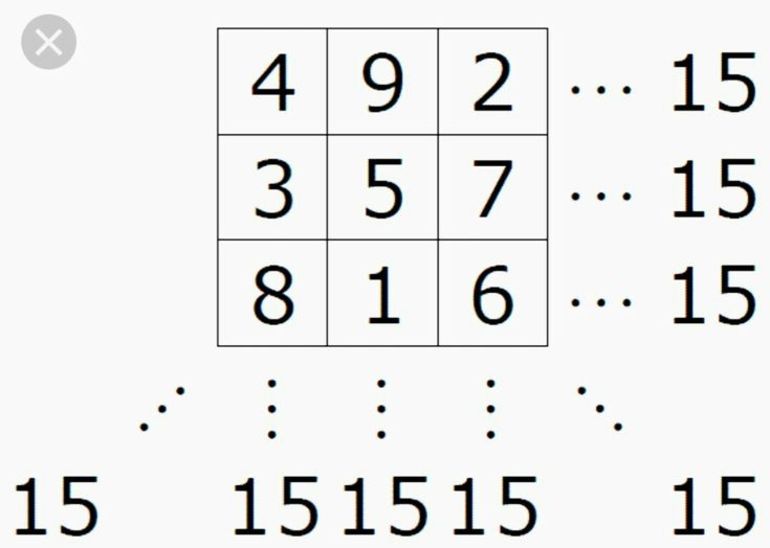
1. Подсчитывается сумма, которая должна получиться в каждой строке. Для этого используется формула: 3 * (32 +1) / 2 = 3 * 10 / 2. Ответом будет число 15.
2. Числа в ячейках расставляются так, чтобы сумма их была равна 15 в каждой строчке. Это требует смекалки и воображения.
3. В средней клетке верхней строки вписывается 1.
4. Каждое следующее число ставится справа по диагонали вверх. Поставить цифру 2 нельзя, так как выше нет строк. Если мысленно добавить сверху ещё один квадрат, цифра 2 окажется в его нижнем правом углу. Значит, цифра 2 вписывается в нижнюю правую клетку.
5. По тому же принципу вписывается цифра 3. Она попадает в среднюю ячейку слева.
6. Если нужная клетка уже занята, очередной символ вписывается ниже предыдущего. Таким образом, 4 ставится под 3.
7. Записывается цифра 5 по диагонали вправо и вверх, а 6 в верхний угол справа.
8. Поскольку место цифры 7 уже занято, она вписывается ниже 6.
9. Восьмёрка занимает место в левом нижнем углу.
10. Оставшуюся клетку занимает девятка.

Общий алгоритм выполнения задания: каждый следующий знак пишется вверх и правее. Если там нет клетки — дорисовывается ещё один воображаемый квадрат. Если ячейка занята — число записывается ниже предыдущего. Таким способом можно составить любой квадрат нечётного порядка, включая самые сложные, с больши́м числом ячеек.

Одинарная чётность

Магические квадраты могут иметь порядок одинарной или двойной чётности. Для каждого случая предусмотрена отдельная методика вычисления. У таблиц одинарной чётности количество клеток в одной строке или столбце делится пополам, но не делится на четыре. Наименьшим квадратом, отвечающим этому требованию, будет прямоугольник 6х6. Фигуру 2х2 построить и заполнить невозможно.

Вычисление магической константы

Первый этап расчётов проводится по формуле [n * (n2 + 1)] / 2, где символом n обозначено число клеток в одном ряду. Если взять за пример квадрат 6х6, расчёт будет выглядеть следующим образом: [6 х (36 + 1)]: 2 = (6 х 37): 2 = 222:2.

Волшебная постоянная прямоугольника со стороной 6 клеток равна 111. Общая сумма чисел от 1 до 36 в каждой строке и в разных направлениях должна быть равна 111.

Рисунок делится на 4 одинаковые части. В каждой будет по 9 клеток (3х3). Каждую часть обозначают латинскими буквами: А — верхняя левая, С — верхняя правая, D — нижняя левая и В — нижняя правая часть. Если квадрат имеет другой размер, n делится на 2, чтобы узнать точную величину каждой из 4 частей.

Дальнейшие действия

Следующий шаг — вписывание в каждую часть ¼ всех чисел. В квадрант А вносятся числа от 1 до 9, в квадрант В — от 10 до 18, в части С — от 19 до 27, в D — от 28 до 36.

Последовательность вписывания такая же, как при заполнении простейшего нечётного квадрата:

1. Минимальное число, которым начинается заполнение ячеек, всегда ставится в верхнем ряду посередине. У каждой части эта ячейка находится отдельно.
2. Каждая часть заполняется как новый математический объект. Даже если есть пустое место в другом квадрате, его в этих случаях игнорируют.

В блоках А и D на этой стадии решения сумма в строках и столбиках будет отличаться от постоянной. Чтобы это исправить, некоторые числа меняют местами между собой.

Алгоритм действий:

1. Начинать нужно с крайней левой клетки в верхней строке. Если фигура имеет размеры 6х6, выделяется только первая верхняя строка части А. В ней должно быть вписано число 8. Если величина таблицы составляет 10х10, выделяют 2 первые клетки в верхнем ряду. В них стоят 17 и 24.
2. Из выделенных клеток формируется промежуточный квадрат. В таблице с количеством строк и столбцов 6х6 он будет состоять из 1 клетки. Его условно обозначают А1.
3. Если размер 10х10, в верхней строке выделяется 2 первые ячейки. Вместе с ними выделяется ещё 2 клетки, во второй строке получается поле из 4 прилежащих друг к другу ячеек.
4. В следующей строке первая ячейка пропускается, затем выделяется столько клеток, сколько было в промежуточной таблице А1. Полученную фигуру можно обозначить А2.
5. Таким же способом строят промежуточный квадрат А3.
6. Эти 3 промежуточных фигуры формируют выделенную область А.
7. Далее переходят в квадрант D и формируют обособленную область D.

Цифры, которые были вписаны в выделенных треугольниках А и D, нужно поменять между собой местами. После этого сумма в каждой строке должна быть одинаковой. Она равняется вычисленной магической константе.

Двойной порядок

Если головоломка имеет порядок двойной чётности, количество окон в каждой горизонтальной строчке или вертикальном столбце должно делиться на 4. Минимальной фигурой с такими свойствами будет таблица 4х4.

Решать магические квадраты двойной чётности следует по тому же алгоритму, что и остальные. Первый шаг при заполнении — вычисление магической константы. Формула применяется та же, что для расчёта других квадратов. Для фигуры со стороной 4 клетки значение константы будет равно 34.

В каждом углу основного поля выделяются промежуточные таблицы. Их размер должен быть равен n/4. Эти области обозначают буквами A, B, C, D, располагая их против хода часовой стрелки. Величина промежуточных фигур зависит от размера исходного квадрата:

1. Если длина стороны составляет 4 ячейки, промежуточные зоны будут иметь по 1 клетке.
2. В таблице 8х8 эти области включают 4 элемента (2х2).
3. В квадрате 12х12 выделяются промежуточные фигуры размером 3х3.

Следующий этап — создание центрального промежуточного квадрата. Величина его стороны должна составлять n/2. Эта фигура не должна накладываться на периферические, но при этом соприкасаться с ними углами.

Далее в квадрат вносят цифры слева направо. Их допускается ставить только в свободные ячейки, которые входят в состав промежуточных областей. Например, при заполнении таблицы 4х4 порядок действий будет таким:

1. В первой сверху строке и первом слева столбце пишется 1. В верхней клетке четвертого столбика — 4.
2. В центр второй горизонтальной строчки ставятся цифры 6 и 7.
3. В четвёртой строке слева пишется 13, а справа — 16.

По этому же принципу цифрами заполняются оставшиеся клетки. Числа проставляются слева в порядке уменьшения. Если всё сделано верно, сумма всех чисел в любой строчке будет одинаковой.

Магические квадраты

Муниципальное общеобразовательное учреждение «Гимназия №41»

Автор: Лабунин Степан, ученик 8 «А» класса

г. Новоуральск, 2012 год.

1. Общие сведения о магических квадратах 4

1.1. Понятие магического квадрата 4

1.2. Из истории магических квадратов 4

1.3. Виды магических квадратов 6

2. Решение магических квадратов 6

2.1. Решение магических квадратов ( метод Баше де Мезирака) 7

2.2. Постановка задачи 8

2.3. Алгоритм решения магических квадратов 8

2.4. Доказательство алгоритма (в алгебраической форме) 9

2.5. Пример решения магического квадрата по алгоритму 10

3. Использование магических квадратов 11

3.1. Разные случаи обобщения магических квадратов 11

3.2. Применение латинских квадратов 12

4. Общие выводы 13

5. Заключение 14

6. Список литературы 15

На занятиях математического кружка мы столкнулись с задачами, связанными с заполнением клеток квадрата по особым правилам. Предложенные числа надо было вписать так, чтобы результат удовлетворял сразу нескольким условиям:

— если сложить все числа в каждой строке,

-если сложить все числа в каждом столбце,

— если сложить все числа в двух диагоналях,

то все эти суммы окажутся равными одному и тому же числу.

Несмотря на то, что задачи отличались исходными числами, порядком чисел, заданностью суммы, все они были подобными, а решения – однотипными.

Возникла идея не просто решить каждое задание, но и придумать общий алгоритм решения, а также найти в литературе исторические сведения о задачах подобного типа.

Выяснилось, что интересующие нас фигуры называются магическими квадратами, известными с древних времён. О них и пойдёт речь в работе.

Цель работы: систематизировать сведения о магических квадратах, разработать алгоритм их решения.

1. Изучить историю возникновения магических квадратов.

2. Выявить виды магических квадратов.

3. Узнать способы решения магических квадратов.

4. Разработать и доказать свой алгоритм решения.

5. Определить применение магических квадратов.

1.Общие сведения о магических квадратах

1.1. Понятие магического квадрата

Большой популярностью даже в наши дни пользуются магические квадраты. Это квадраты, в каждую клетку которых вписаны числа так, что суммы чисел вдоль любой горизонтали, любой вертикали и любой диагонали равны. Самым известным считается магический квадрат, изображённый на гравюре немецкого художника А. Дюрера «Меланхолия» (приложение 1).

1.2. Из истории магических квадратов

Числа настолько вошли в жизнь человека, что им стали приписывать всякие магические свойства. Уже несколько тысяч лет назад в Древнем Китае увлеклись составлением магических квадратов. При археологических раскопках в Китае и Индии были найдены квадратные амулеты. Квадрат был разделён на девять маленьких квадратиков, в каждом из которых были написаны числа от 1 до 9. Замечательно, что суммы всех чисел в любой вертикали, горизонтали и диагонали были равны одному и тому же числу 15 (рисунок 1).

В средние века магические квадраты были очень популярны. Один из магических квадратов изображен на гравюре знаменитого немецкого художника Альбрехта Дюрера, «Меланхолия». В 16 клетках квадрата размещены цифры от 1 до 16, а сумма чисел по всем направлениям равна 34. Любопытно, что два числа в середине нижней строки указывают на год создания картины – 1514 г. Получение магических квадратов было популярным развлечением среди математиков, создавались огромные квадраты, например, 43×43, содержащий числа от 1 до 1849, причём обладающие помимо указанных свойств магических квадратов, ещё и многими дополнительными свойствами. Были придуманы способы построения магических квадратов любого размера, однако до сих пор не найдена формула, по которой можно было бы найти количество магических квадратов данного размера. Известно, и это вы можете легко показать сами, что магических квадратов размером 2×2 не существует, магических квадратов 3×3 ровно один, остальные такие квадраты получаются из него поворотами и симметриями. Магических квадратов 4×4 уже 800, а количество квадратов 5×5 близко к четверти миллиона.

1.3. Виды магических квадратов

Магический (волшебный квадрат) — это квадратная таблица nxn, заполненная n2 числами таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях одинакова.

Полумагический квадрат — это квадратная таблица nxn, заполненная n2 числами таким образом, что суммы чисел равны только в строках и столбцах.

Нормальный – магический квадрат, заполненный целыми числами от 1 до n2.

Ассоциативный (симметричный) — магический квадрат, у которого сумма любых двух чисел, расположенных симметрично относительно центра квадрата, равна n2 + 1.

Дьявольский (пандиагональный) магический квадрат — магический квадрат, в котором также с магической константой совпадают суммы чисел по ломаным диагоналям (диагонали, которые образуются при сворачивании квадрата в тор) в обоих направлениях.

Существует 48 дьявольских магических квадратов 4×4 с точностью до поворотов и отражений. Если принять во внимание еще и их дополнительную симметрию — торические параллельные переносы, то останется только 3 существенно различных квадрата (рисунок 2).

Пандиагональные квадраты четвёртого порядка обладают рядом дополнительных свойств, за которые их называют совершенными. Совершенных квадратов нечётного порядка не существует. Среди пандиагональных квадратов двойной чётности выше 4 имеются совершенные.

Пандиагональных квадратов пятого порядка 3600. С учётом торических параллельных переносов имеется 144 различных пандиагональных квадратов.

2.Решение магических квадратов

2.1Решение магических квадратов (метод Баше де Мезирака)

Правила построения магических квадратов делятся на три категории в зависимости от того, каков порядок квадрата: нечетен, равен удвоенному нечетному числу или равен учетверенному нечетному числу. Общий метод построения всех квадратов неизвестен, хотя широко применяются различные схемы. Найти все магические квадраты порядка n удается только для n ≤ 4.

Для решения нормальных магических квадратов сколь угодно большого размера воспользуемся методом, описанным в 1612 г. французским математиком Клодом Баше де Мезираком. Русский перевод его книги был издан в Петербурге в 1877 г. под названием «Игры и задачи, основанные на математике».

Магический квадрат удобно строить на бумаге в клетку. Пусть n-нечётное число, и нужно построить квадрат nхn с числами от 1 до n2 , действуем поэтапно.

1. Все числа от 1 до n2 записываем в клетки по диагонали (по n чисел в ряд), чтобы образовался диагональный квадрат.

2. Выделяем в его центре квадрат nхn. Это и есть основа (ещё не все клетки заполнены) будущего магического квадрата.

3. Каждый находящийся вне центрального квадрата числовой «уголок» аккуратно переносим внутрь — к противоположной стороне квадрата. Числа этих уголков должны заполнить все пустые клетки. Магический квадрат построен.

Приведём пример заполнения квадрата 3х3 числами от 1 до 9. Для этого к квадрату пририсуем дополнительные клетки, чтобы получить диагонали. Сначала заполним диагональные клетки числами от 1 до 9 (рисунок 3), потом в пустые клетки квадрата «загнём уголки» внутрь к противоположной стороне (рисунок 4).

Рисунок 3. Рисунок 4.

2.2. Постановка задачи.

Опишем свой способ решения магических квадратов. Остановимся на изучении математической модели магических квадратов 3×3.

Общая формулировка задачи.

Имеются девять чисел. Необходимо расставить их в клетки квадрата размера 3×3, так чтобы по любой вертикали, горизонтали и диагонали суммы чисел были равны.

2.3. Алгоритм решения магического квадрата

Словесное описание алгоритма

1. Упорядочить числа по возрастанию.

2. Найти центральное число (пятое по порядку).

3. Определить пары по правилу: 1 пара — первое число и девятое,

2 пара — второе число и восьмое,

3 пара — третье число и седьмое,

4 пара – четвёртое число и шестое.

4. Узнать сумму чисел (S), которая должна получиться при сложении чисел по каждой вертикали, горизонтали, диагонали: сложить самое маленькое, центральное, самое большое число, т. е. числа 1 пары с центральным числом.

5. Поставить в центр квадрата центральное число.

6. По центральной горизонтали (или вертикали) в свободные клетки вписать первую пару чисел.

7. По любой диагонали записать вторую пару чисел (так чтобы большее число первой пары оказалось в столбике с меньшим числом второй пары).

8. Вычислить число, которое надо записать в один из крайних столбиков, по правилу:

из S вычесть сумму двух чисел, содержащихся в клетках столбика, получить число.

9. По диагонали к полученному числу записать второе число его пары.

10. Вписать в оставшиеся клетки последнюю пару чисел по правилу: большее число из пары вписать в строку с меньшим, а меньшее в оставшуюся пустую клетку.

2.4. Доказательство правильности заполнения магического квадрата

(Решение задачи в общем виде)

Докажем, что суммы чисел, находящихся по вертикалям, горизонталям и диагоналям квадрата в результате выполнения алгоритма, получатся равные.

Пусть после упорядочения каждое последующее число отличается от предыдущего на постоянную величину х. Выразим все числа через а1 (наименьшее число) и х:

Пусть магический квадрат заполнен по предложенному алгоритму.

Докажем, что суммы чисел, расположенных по горизонтали, вертикали и диагонали квадрата, равны S.

Получили одинаковые суммы. Утверждение доказано.

Числа, организованные таким образом, образуют арифметическую прогрессию. В этой последовательности (после упорядочения) а1 – это первый член арифметической прогрессии, х – это разность арифметической прогрессии. Для чисел, не составляющих арифметическую прогрессию, алгоритм не действует.

2.5. Пример решения магических квадратов

Даны числа:5,2,4,8,1,3,7,9,6. Заполнить магический квадрат данными числами.

2. Получили центральное число 5.

3. Пары:1 и 9, 2 и 8, 3 и 7, 4 и 6.

4. S = 5+1+9=15 – сумма.

Данный алгоритм существенно отличается от метода Баше де Мезириака. С одной стороны он требует дополнительных вычислений (недостаток метода), с другой стороны в нашем методе не нужны дополнительные построения (диагональный квадрат). Более того, метод применим не только к последовательным натуральным числам от 1 до 9, но и к любым девяти числам, являющимися членами арифметической прогрессии, в чём мы видим его преимущества. Кроме того, автоматически определяется магическая константа – сумма чисел по каждой диагонали, вертикали, горизонтали.

3. Использование магических квадратов

3.1. Разные случаи обобщения магических квадратов

Задачи составления и описания магических квадратов интересовали математиков с древнейших времён. Однако полного описания всех вех возможных магических квадратов не получено и до сего времени. С увеличением размеров (числа клеток) квадрата быстро растёт количество возможных магических квадратов. Среди квадратов больших размеров есть квадраты обладающими интересными свойствами. Например, в квадрате на рисунке № 5 равны между собой не только суммы чисел в строках столбцах и диагоналях, но и суммы пятёрок по «разломанным» диагоналям, связанными на рисунке цветными линиями.

Рисунок 5. Рисунок 6.

Латинским квадратов называется квадрат n x n клеток, в которых написаны числа 1, 2, …, n, притом так, что в каждой строке и каждом столбце встречаются все эти числа по одному разу. На (рисунке 6) изображены два таких латинских квадрата 4×4. Они обладают интересной особенностью: если один квадрат наложить на другой, то все пары получившихся чисел оказываются различными. Такие пары латинских квадратов называются ортогональными. Задачу отыскания ортогональных латинских квадратов впервые поставил Л. Эйлер, причём в такой занимательной формулировке: «Среди 36 офицеров поровну уланов, драгунов, гусаров, кирасиров, кавалергардов и гренадёров и кроме того поровну генералов, полковников, майоров, капитанов, поручиков и подпоручиков, причём каждый род войск представлен офицерами всех шести рангов. Можно ли выстроить этих офицеров в каре 6×6 так, чтобы в любой колонне встречались офицеры всех рангов?» (приложение 2).

Л. Эйлер не смог найти решения этой задачи. В 1901 г. было доказано, что такого решения не существует.

3.2. Применение латинских квадратов

Магические и латинские квадраты близкие родственники. Теория латинских квадратов нашла многочисленные применения, как в самой математике, так и в её приложениях. Приведём такой пример. Пусть мы хотим испытать два сорта пшеницы на урожайность в данной местности, причём хотим учесть влияние степени разреженности посевов и влияние двух видов удобрений. Для этого разобьём квадратный участок на 16 равных частей (рисунок 7). Первый сорт пшеницы посадим на делянках, соответствующих нижней горизонтальной полосе, следующий сорт посадим на четырёх делянках, соответствующих следующей полосе и т. д. (на рисунке сорт обозначен цветом.)

При этом максимальная густота посевов пусть будет на тех делянках, которые соответствуют левому вертикальному столбцу рисунка, и уменьшается при переходе вправо (на рисунке это соответствует уменьшению интенсивности цвета.) Цифры же, стоящие в клетках рисунка, пусть означают: первая – количество килограммов удобрений первого вида, вносимая на этот участок, а вторая — количество вносимого удобрения второго вида. Не трудно понять, что при этом реализованы все возможные пары сочетаний как сорта и густоты посева, таки других компонентов: сорта и удобрения первого вида, удобрений первого и второго видов, густоты и удобрений второго вида.

Использование ортогональных латинских квадратов помогает учесть все возможные варианты в экспериментах в сельском хозяйстве, физике, химии и технике.

В ходе выполнения работы я познакомился с различными видами Магических квадратов, узнал способ решения нормальных магических квадратов методом Баше де Мезирака. Так как наше решение магических квадратов 3х3 отличалось от указанного метода, но позволяло каждый раз правильно заполнить клетки квадрата, то возникло желание разработать собственный алгоритм. Этот алгоритм подробно описан в работе, доказан в алгебраической форме. Оказалось, что он применим не только к нормальным квадратам, но и к квадратам размером 3х3, где числа составляют арифметическую прогрессию. Нам удалось также найти примеры применения магических и латинских квадратов.

Я научился: решать некоторые магические квадраты, разрабатывать и описывать алгоритмы, доказывать утверждения в алгебраической форме. Я узнал новые понятия: арифметическая прогрессия, магический квадрат, магическая константа, изучил виды квадратов.

К сожалению, ни мой разработанный алгоритм, ни метод Баше де Мезирака не позволяют решать магические квадраты размера 4х4. Поэтому мне захотелось в дальнейшем составить алгоритм решения для таких квадратов.

В данной работе изучались магические квадраты, рассматривалась история их происхождения. Были определены виды магических квадратов: магический или волшебный квадрат, полумагический квадрат, нормальный, ассоциативный, дьявольский магический квадрат, совершенный.

Среди существующих способов их решения выбран метод Баше де Мезириака, он апробирован на примерах. Кроме того, для решения магических квадратов 3х3 предложен собственный алгоритм решения, приведено математическое доказательство в алгебраической форме.

Предложенный алгоритм существенно отличается от метода Баше де Мезириака. С одной стороны, он требует дополнительных вычислений (недостаток метода), с другой стороны, не нужны дополнительные построения. Метод применим не только к последовательным натуральным числам от 1 до 9, но и к любым девяти числам, являющимися членами арифметической прогрессии, в чём мы видим его преимущества. Кроме того, автоматически определяется магическая константа – сумма чисел по каждой диагонали, вертикали, горизонтали.

В работе представлено обобщение магических квадратов – латинские квадраты и описано их практическое применение.

Данная работа может быть использована на уроках математики в качестве дополнительного материала, а также на занятиях кружка и в индивидуальной работе с учащимися.

6. Список литературы

1. Загадки мира чисел / Сост. – Д.: Сталкер, 1997.-448с.

2. Энциклопедический словарь юного математика / Сост. – М.: Педагогика, 1989 –352с.: ил.

3. Энциклопедия для детей. Т11. Математика / Глав. ред. – М.: Аванта+, 2000 – 688с.: ил.

4. Я познаю мир : Детская энциклопедия : Математика / Сост. – и др. – М.: АСТ, 1996. – 480с.: ил.

5. Задачи для внеклассной работы по математике в V-VI классах: Пособие для учителей/ Сост. . Под ред. , . – М.: МИРОС, 1993. – 72 с.: ил.

Магический квадрат — виды, правила и примеры решения

Среди поклонников логических игр большой популярностью пользуется магический квадрат. Он представляет собой таблицу, заполненную особым образом цифрами. Причём сумма чисел одинакова по всем направлениям. Эту величину принято называть константой. Существует множество вариантов таких головоломок разной степени сложности.

История и современное применение

Первые подобные таблицы использовались ещё в Древней Греции и Китае. Это подтверждено археологическими находками. Арабы называли квадраты магическими, так как верили, что они обладают волшебными свойствами и могут защитить от многих напастей.

В середине XVI в. вопросом о том, как работает магический квадрат, заинтересовались математики в Европе. Они начали активно исследовать загадочные сочетания цифр. Учёные стремились вывести общие принципы построения квадратов и найти всё множество возможных вариантов.

В современной общеобразовательной школе разные виды магических квадратов используются на уроках математики. Они способствуют развитию логического мышления и вызывают у детей живой интерес.

С их помощью школьники учатся планировать свою работу и контролировать её. В клетки можно вписывать не только отдельные цифры, но и математические выражения. Задачи на эту тему часто предлагаются на математических олимпиадах. Решать такие числовые задачи можно и онлайн.

Квадрат нечётного порядка

Среди несложных магических квадратов по математике выделяют разновидности чётного и нечётного порядка. Первая группа подразделяется на таблицы одинарной и двойной чётности.

Начальным шагом во всех случаях будет определение магической константы. Делается это с помощью специальной формулы [n * (n2 + 1)] / 2. Разобраться с принципом решения задачи этого класса можно на самом простом примере. Для этого выстраивается таблица из 9 ячеек. В неё нужно расставить цифры от 1 до 9. Дальнейший алгоритм: